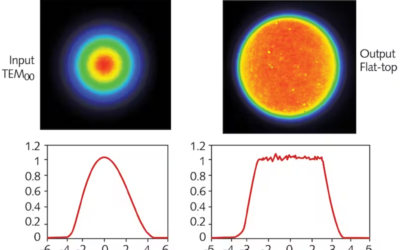
Paraxial Lenses
Paraxial lenses are a simplified model used to analyze and design optical systems, particularly lenses. In the paraxial approximation, light rays passing through a lens are assumed to be close to the optical axis and at small angles with respect to it. This approximation allows for the use of simple mathematical equations to describe the behavior of light as it passes through the lens.
Paraxial lenses are characterized by their focal length and their optical power, which is the reciprocal of the focal length and is measured in diopters (D). A positive power indicates a converging lens, while a negative power indicates a diverging lens.
Using the paraxial approximation, various calculations can be made to determine the behavior of light rays as they pass through a lens, such as an image formation, magnification, and the relationship between object and image distances. These calculations are based on the thin lens equation, which relates the object distance (distance from the lens to the object), the image distance (distance from the lens to the image), and the focal length of the lens.
While the paraxial approximation is a simplification and does not account for all the optical effects that occur in real lenses, it provides a useful starting point for understanding and designing optical systems. It is particularly valuable in situations where the light rays are close to the optical axis and at small angles, which is often the case in many practical applications of lenses.
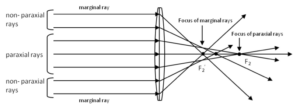
Figure 1. The figure illustrates the concept of paraxial and marginal rays in an optical system. Paraxial rays are close to the optical axis and at small angles with respect to it. These rays are used in the paraxial approximation to analyze the behavior of light through the lens. Marginal rays (right) are at the outermost points of the object. These rays define the extreme limits of the aperture or field of view and help determine the maximum angles of light entry or exit. Image from physicsbootcamp
While the paraxial approximation is a useful tool for the initial analysis and design of optical systems, it has certain limitations and disadvantages. Here are some of the disadvantages of using paraxial lenses:
- Ignoring higher-order aberrations: The paraxial approximation neglects higher-order aberrations such as spherical aberration, coma, astigmatism, and distortion. These aberrations can significantly impact the image quality and can cause blurring, distortion, or other undesirable effects. Therefore, the paraxial model may not accurately represent the actual performance of a lens.
- Limited accuracy off-axis: The paraxial approximation assumes that light rays are close to the optical axis and at small angles. As the rays deviate from the axis or at larger angles, the paraxial model becomes less accurate. This limitation is particularly relevant for wide-angle or high-magnification optical systems where off-axis aberrations become more significant.
- Inaccurate for thick lenses: Paraxial lenses assume that the lens is thin compared to its radius of curvature. When dealing with thick lenses, the paraxial model may not accurately represent the behavior of light rays passing through the lens. Thick lenses can exhibit additional optical effects such as coma, lateral color, and transverse magnification.
- Limited applicability to complex systems: Paraxial lenses are most suitable for simple optical systems with a single lens or a few thin lenses in close proximity. They are less applicable to complex optical systems that involve multiple lenses, mirrors, or other optical components. In such cases, the paraxial approximation may not capture the interactions and complexities of the system accurately.
- Excludes diffraction effects: The paraxial model does not consider the wave nature of light and the diffraction effects that occur when light encounters small apertures or diffractive elements. Diffraction effects become increasingly important as the size of the aperture or the wavelength of light becomes comparable to the scale of the system.
Despite these limitations, the paraxial approximation remains a valuable tool for initial analysis and design due to its simplicity and ease of calculation. However, for accurate and comprehensive analysis of complex optical systems or high-precision applications, more advanced techniques such as ray tracing or physical optics simulations are necessary.